Bad and Good Benchmarking

So, when you have a bunch of ingredients but nothing special in mind to cook, what do you do? You make a stew. That’s what I’m doing today.
All code from this post is available on GitHub: https://github.com/JonasJSchreiber/Primitive-Benchmarking

Down the Rabbit Hole

It started with a YouTube video on Dynamic Programming. In it, the professor mentions a O(log(n)) Fibonacci solution. That’s all it took…
I started small, by implementing DP in a Fibonacci sandbox, and using a very primitive form of benchmarking to test how big of an improvement I saw by running one million iterations of finding the 46th Fiboacci number (the largest Fibonacci number that’s still an integer).
I did this in three ways: the linear approach, the recursive approach with memoization, and the “log(n)” approach – matrix multiplication.

Iterative approach 1000000 times took 7483258 ns
Lookup from HashMaps 1000000 times took 7790283 ns
Matrix multiplication approach 1000000 times took 16796349 ns

Deceptive, and we’ll dig into why later.

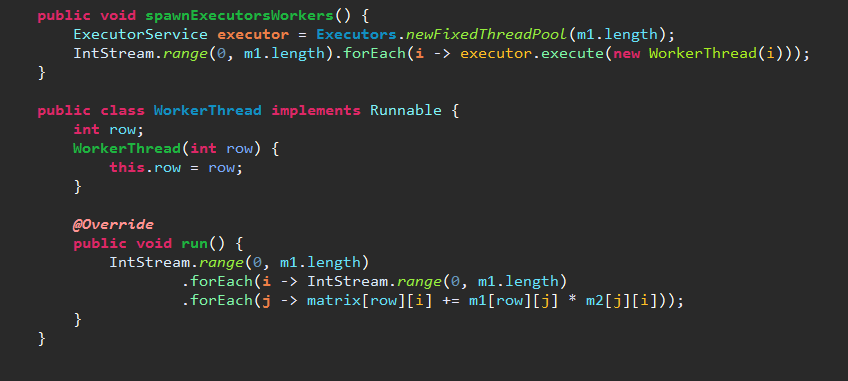
A Better Test Using Concurrency

The task: multiply two 1000 x 1000 matrices. Do it in a single threaded way, and a multi-threaded way. Explore Java’s Futures and Executors frameworks. Get some experience with Lambda syntax.

Benchmark results were impressive.

Multi Threaded Execution with Executors Took: 1304ms
Multi Threaded Execution with Futures Took: 1551ms
Single Threaded Execution Took: 7581ms

My machine is a 6 core CPU. So taking the 7581ms time, dividing by 6 should be the lower bound on what it can achieve.
Assuming that statement is correct, my implementation using the executors squeezes 96.8% of the theoretical headroom out of this problem. Awesome!

Why Fibonacci DP Results Were Misleading

So, dynamic programming is basically taking a problem and breaking it into n subproblems, and intelligently re-using the answers to subproblems so that you never have to perform the same computation twice.
This works out well in most cases, path finding algorithms, tree traversal problems, etc. It even works “well” for my use case, Fibonacci. It just so happens that Hash lookups are actually slower on my machine than adding two numbers together 46 (-2) times.
Here is my example. In it, I get the runtime for an iterative approach to Fibonacci, the matrix multiplication approach, and, rather than even performing the recursive approach, I simply do one has lookup. The answer is essentially stored in a HashMap, and retrieved, a million times.

Why is retrieving a value from a hash map taking so long? Let’s look at the source code.

Aren’t HashMap lookups supposed to take O(1) time?
Well, it turns out, not quite. Theoretically, this algorithm take O(1 + n/k) where k is the number of buckets. If two elements are inserted into the hash table and wind up in the same bucket, you need to look through each element in the bucket for yours.
That’s theoretical. In reality, while I doubt there are too many collisions, you must still perform the hashing function on your object, get the bucket, check to see if the first entry in the bucket is yours, and return it. All of this takes time.

What Makes a “Good” Benchmark?

For one thing, doing a task one million times adds a bunch of overhead involved with the testing framework and class instantiation, etc. The biggest consumer of your time may not even be the actual work you’re doing.
But critiquing my own failed benchmark with Fibonacci and comparing against the matrix multiplication benchmark is not going to do this topic justice. For that, I’d suggest this thread on StackOverflow. The answer by Eugene Kuleshov is pretty comprehensive.